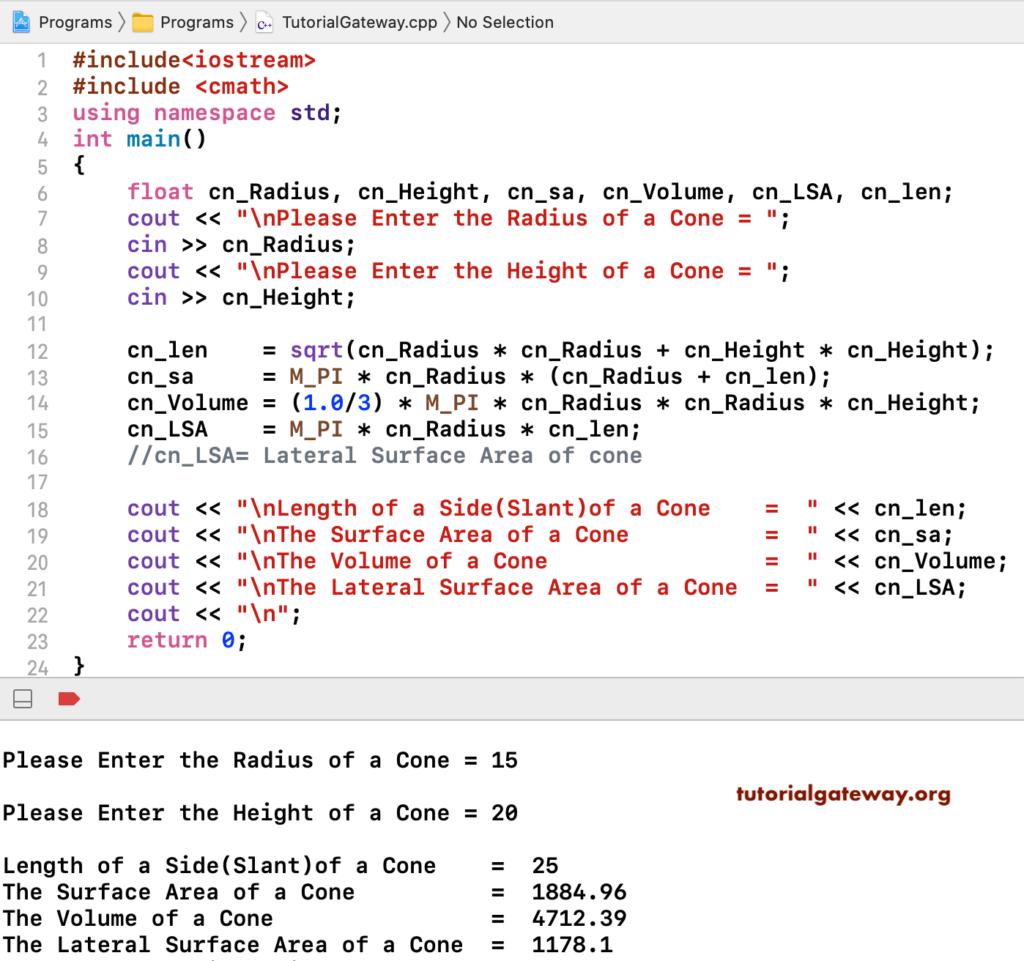
Given slant height, height and radius of a cone, we have to calculate the volume and surface area of the cone. In simple words, a cone is a pyramid with a circular base. A cone has a three-dimensional shape so calculating its volume can seem a little complicated. To help you understand better, in this article we explain what a cone is as well as how to calculate its volume. We detail the steps one by one and the formulas you have to use to calculate the volume of a cone with accurate examples.
In a cone, the perpendicular length between the vertex of a cone and the center of the circular base is known as the height of a cone. A cone's slanted lines are the length of a cone along the taper curved surface. All of these parameters are mentioned in the figure above. This online calculator will calculate the various properties of a right circular cone given any 2 known variables.
The term "circular" clarifies this shape as a pyramid with a circular cross section. The term "right" means that the vertex of the cone is centered above the base. Using the term "cone" by itself often commonly means a right circular cone. A cone folded flat forms a sector of a larger circle.Imagine a cone without its base, made out of paper. You then roll it out so it lies flat on a table.
You will get a shape like the one in the diagram above. It is a part of a larger circle, whose radius is equal to the slant height of the cone. The arc length of the sector is equivalent to the circumference of the cone base.
This calculator is for a particular type of cone called a right cone . It has a circular base, and the vertex is directly above the center of the base. Therefore, the angle made between the base and an imaginary line between the base and the vertex is 90°, commonly known as a right angle.
A cone is a three-dimensional figure with one circular base. A curved surface connects the base and the vertex. The slant height of a right cone is the length of the segment from the vertex of the cone to the circle of the base. Slant height is not defined for oblique cones. Enter the height of the cone or the slant height of the cone, depending on which one is known.
The height is the perpendicular distance between the cone tip and the center of the circular base. The slant height is the distance between the tip and the outside edge of the base. Since slant height is undefined for an oblique cone, there are no formulas for the areas of oblique cones. Where r is the radius of the circular base, and s is the slant height of the cone. What is the volume of the cone with a diameter that is $50$ ft long and a height of $12$ ft?
What is the volume of the cone with a radius that is $12$ inches long and a height of $20$ inches? Given radius and total surface area calculate the height, slant height, volume and lateral surface area. Given radius and lateral surface area calculate the height, slant height, volume and total surface area. Given radius and slant height calculate the height, volume, lateral surface area and total surface area.
Enter a value for the radius of the circular base. Remember that the radius is half of the diameter of a circle. You can choose different units of length, depending on the problem or measurement taken.
Alternatively, you can enter the circumference of the circular base instead. Before we explain how to use our surface area of a cone calculator, let's first define what type of cone you can use it on. A generic cone shape consists of a circular or oval base and a vertex above the base connected to the perimeter of the base shape.
Given slant height and lateral surface area calculate the radius, height, volume, and total surface area. Given radius and volume calculate the height, slant height, lateral surface area and total surface area. Given radius and height calculate the slant height, volume, lateral surface area and total surface area. Generally, the volume of a three-dimensional solid is the amount of space it occupies and it's measured in cubic units. This surface area of a cone calculator will help you calculate the surface area of any right cone.
In the text below, we will show you the surface area of a cone formula and how to derive it. After using our calculator and reading this article, you'll be super confident about how to find the surface area of a cone. But the trick is to figure out how to design a 2-D net for the cone.
Did you know that the 2-D net for a cone is a sector of a circle? Here, the circle we are talking about has radius s . So we know the radius of the sector is s, not r. But the big question is, how big is the angle of the sector?
How To Find Height Of Cone Given Volume And Radius The amount of the circumference of the sector is the same as the whole circumference of the cone's base, namely, 2𝜋r. The volumes of a cone and a cylinder are related in the same way as the volumes of a pyramid and a prism are related. If the heights of a cone and a cylinder are equal, then the volume of the cylinder is three times as much as the volume of a cone. The volume V of a cone with radius r is one-third the area of the base B times the height h .
The volume of a 3 -dimensional solid is the amount of space it occupies. Be sure that all of the measurements are in the same unit before computing the volume. The radius and slant height of a cone are 12 mm and 25 mm. respectively.
Drag either orange dot in the top figure and note how the slant height is calculated from the radius and altitude. Drag the orange dots to adjust the radius and height of the cone and note how the slant height changes. Notice that the slant height is part of a right triangle.
Given height and volume calculate the radius, slant height, lateral surface area and total surface area. Given height and slant height calculate the radius, volume, lateral surface area and total surface area. We now have two equations to calculate the surface area of a right cone, depending on what parameters are known. Let's start by calculating the area of the circular base.
Find the total surface area of a right cone if the radius is 6 inches and the slant height is 10 inches. The radius of the cone is the radius of the base. The altitude of the cone is the perpendicular segment from the vertex to the plane of the base.
The height of the cone is the length of the altitude. Where r is the radius of the circular base, and h is the height . In this article, we will discuss how to use the volume of a cone formula to calculate the volume of a cone. Drag the orange dots to set the radius and height of the cone. The radius becomes the leg of the right triangle, and the slant height becomes the hypotenuse of the right triangle. Remember to always state the volume in cubic units because you've calculated the volume of a three-dimensional space.
If you need to calculate the surface areas of other 3D geometric shapes, why not try out our surface area calculator. This tool cannot be used for oblique cones, where the vertex is off-center. Find the total surface area of a cone, whose base radius is 3 cm and the perpendicular height is 4 cm.
Find the lateral surface area of a right cone if the radius is 4 cm and the slant height is 5 cm. So, the formulas for their surface areas and volume are related. The axis of the cone is the segment whose endpoints are the vertex and the center of the base.
If the axis is perpendicular to the plane of the circle, the cone is a right cone otherwise it is an oblique cone . It consists of a base having the shape of a circle and a curved side ending up in a tip called the apex or vertex. The slant height which is the distance from the top, down the side, to a point on the base circumference. To find the total surface area of the cone, we need slant height of the cone, instead the perpendicular height. From the figure, the radius of the cone is 8 cm and the height is 18 cm. Find the volume of a cone whose altitude is 15 m and whose radius is 8 m.
Since the base of a cone is a circle, we substitute 2 π r for p and π r 2 for B where r is the radius of the base of the cone. Find the volume of the cone of radius, 5 cm, and height, 10 cm. Like all other volumes, the volume of a cone is also expressed in cubic units.
Calculations are based on algebraic manipulation of these standard formulas. Check out this perimeter of a rectangle calculator and quickly estimate the necessary parameters of a rectangle. The average calculator calculates the average of a set of up to 30 numbers. Now you know how to find the surface area of a cone and the equations that power this surface area of a cone calculator. Later, we will add this base area equation to the equation we will derive next for the lateral area of a right cone.
A cone has a radius of 3cm and height of 5cm, find total surface area of the cone. Figuring out how many cones it will take to fill the cylinder. Round to the nearest tenth of a cubic centimeter. Remember, the formulas for the lateral surface area of a pyramid is 1 2 p l and the total surface area is 1 2 p l + B . To get the time take for the silo to be empty, divide the volume of the silo by the flow rate of the cereals. Let's gain an insight into the volume of a cone formula by working out a few example problems.
Where V is the volume, r is the radius and h, is the height. The vertical height which is the perpendicular distance from the top down to the base. The surface area of the right cone will then be displayed.
You can change the units of the area, depending on your taste or the overall size of the cone. Height and radius of the cone is 5 yard and 7 yard. Find the lateral surface area of the given cone. Now, you will need to find the area of the cone itself.
In order to do this, you must measure the side of the cone. Make sure you use the same form of measurement as the radius. A conical storage tank has a diameter of 5 m and a height of 10 m. Top Ten Math Cheats The following is a helpful list of math cheat sheets.
I have included a short explanation of the topics covered in the... Use the following additional formulas along with the formulas above.